Today we’re going to cover:

• Interference patterns
• Conditions required for 2-source interference
• Equation λ = ax/D

Let’s go!

---

What happens when a wave is sent through 2 slits?
It forms an INTERFERENCE PATTERN like so:

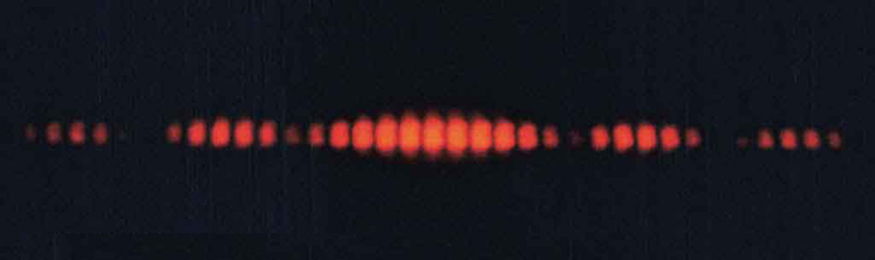
What are the conditions required in order for this 2-source interference pattern to be observed?

• Waves must be COHERENT
• 2 sources emit circular waves (radially)

---

What is coherence?
2 wave sources are said to be coherent sources when they:

• Emit only 1 frequency (for light, monochromatic)
• Have the same frequency
• Have a constant phase relationship (they are in phase)

How do you ensure 2 sources are coherent?

For sound/water waves	Use 2 oscillators or speakers linked to the same wave generator (oscillator & amplifier).
For light	Use a single monochromatic light source. To ensure that there is only 1 frequency of EM waves   Diffract the waves through a single slit, then diffract the waves through 2 slits to ensure that the 2 waves are in phase.

---

1 classic example of 2-source interference is Young’s Double Slit Experiment.

Here, a monochromatic light source is put behind a single slit, diffracting the light waves further into 2 slits (which act as the 2 sources).

The interference pattern can be seen on a screen – this experiment was one of the first to show that light had wave properties.

The pattern is described as a FRINGE pattern, consisting of bright & dark fringes:

Bright fringes	Places on the screen where constructive interference occurs
Dark fringes	Places on the screen where destructive interference ocurs

---

What affects the distance between fringes on this pattern?
This distance is labelled as x, & is affected by:

FACTOR	SYMBOL	EFFECT
Wavelength of light	λ	Higher λ = larger x
Distance between coherent sources	a	Higher a = larger x
Distance from sources to screen	D	Higher D = smaller x

The equation relating them all:

OR, rearranged to express x:

---

A brief recap on the reason behind the pattern:

Interference at the screen is caused by the path difference between waves from the 2 sources to every point on the screen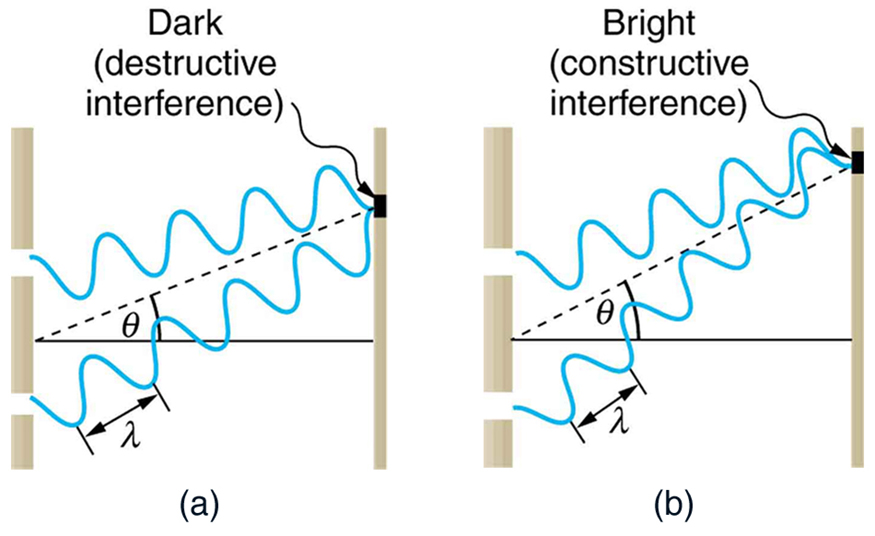
If the path difference is a whole multiple of λ, constructive interference occurs	For Δd = nλ: Constructive interference
If the path difference is a whole multiple of λ/2, destructive interference occurs	For Δd = nλ/2: Destructive interference
The order of the fringe from the centre is related to the path difference: The further the position on the screen from the centre, the larger the path difference.	The 0th bright fringe (in the centre) has 0 path difference 1st bright fringe has a path difference of λ 2nd bright fringe has a path difference of 2λ …etc.

---

What if we use non-monochromatic light (white light) for the double slit experiment?
A clear fringe pattern will not be seen.

White light is made up of many different frequencies of light.
When all of these pass through the double slit, they form their own individual patterns.

The patterns overlap on each other, resulting in mostly white light surrounding coloured fringes near the centre.

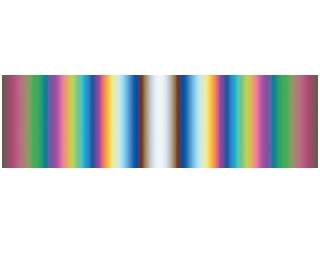
⇐ Previous in Physics: Measuring the Speed of Sound using Stationary Waves
⇒ Next in Physics: Diffraction