Today we will be covering:
- Stress
- Strain
- Young Modulus
- Graphs of Deformation (Stress-Strain)
- Elastic & Plastic Deformation
Let’s go!
Objects under deformation (whether it is tensile or compressive) experience STRESS & STRAIN.
These depend on the force, cross-sectional area, initial length, extension, & rigidity of the material.
What is Stress?
Force acting per unit perpendicular cross-sectional area.
It is denoted by the symbol σ (sigma).
σ = F/A
In units, N m-2 or Pa (Pascals, like pressure).
If the object’s cross-sectional area remains constant, stress is proportional to load.
What is Strain?
Change in length (extension, e) per unit original length.
It is denoted by the symbol ε (epsilon).
ε = e/lo
It has NO UNITS: it is only a ratio of two lengths.
Strain can presented as an ABSOLUTE VALUE:
a/b = 0.01/1.00 = 0.01
OR as a PERCENTAGE:
a/b x 100 = 0.01/1.00 x 100 = 1%
What is the Young Modulus?
Stress experienced per unit strain of a body when it is subjected to a constant force.
It is denoted by the letter E.
The Young Modulus represents the RIGIDITY of the material used to make the body.
Different materials have different Young Moduli, & 2 objects made of the same material both have the SAME Young Modulus (rigidity).
Young Modulus = stress/strain
E = σ/ε
In units, N m-2 or Pa (Pascals).
Determining E
You can carry out a tensile test & plot a Stress-Strain graph (see below) to find the Young Modulus of an object:
E = σ/ε
σ = Eε
With stress as the y-axis, strain as the x-axis, the gradient is the Young Modulus.
You can also use the Spring Constant of an object to find the Young Modulus of its material (if you also know the initial dimensions of the object):
E = σ/ε
E = F/A x lo/e
E = Flo/Ae
Since F/e = k,
E = k(lo/A)
What is Elastic & Plastic Deformation?
| Elastic Deformation | Plastic Deformation |
| Deformation wherein an object can return to its original size after the applied load is removed.
The object tends to extend proportionally to the force applied. |
Deformation wherein an object cannot return to its original size after the applied load is removed.
The object extends more per unit increase in load than elastic deformation. |
Stress-Strain Graph

What’s happening here?
- OA: Initially, the object extends according to Hooke’s Law.
The stress (force per unit area) is proportional to the strain (ratio of extension). - A: It reaches the proportionality limit, & no longer obeys Hooke’s Law above that.
- L: It reaches the elastic limit, & the object can no longer return to its original size after load is removed
- B: It reaches the yield point, & the object begins to behave plastically.
- C: It reaches the maximum stress.
- D: It reaches the ultimate tensile stress. The object breaks.
| Proportionality Limit | Maximum point of extension where a body obeys Hooke’s Law |
| Elastic Limit | Maximum point of extension where a body can still behave elastically (return to its original size after an applied load is removed) |
| Yield Point | Point at which a material begins to behave plastically (extends more per unit increase in load than before) |
| Maximum Stress | Maximum stress which the object experiences |
| Breaking Stress / Ultimate Tensile Stress |
Maximum stress which can be applied to a material before it breaks |
Graphs of Ductile, Brittle & Polymeric Materials
| Material | Behaviour | Graph |
| Ductile |
|
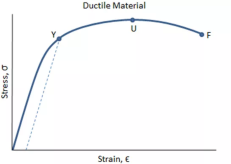 |
| Brittle |
|
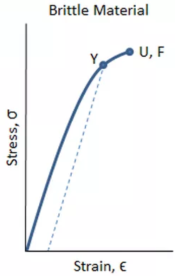 |
| Polymeric |
|
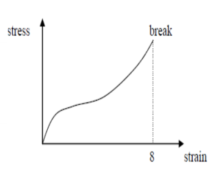 |
⇐ Previous in Physics: Deformation & Springs
⇒ Next in Physics: Strain Energy
